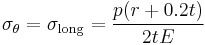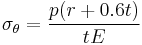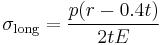Pressure vessel
A pressure vessel is a closed container designed to hold gases or liquids at a pressure substantially different from the ambient pressure.
The pressure differential is dangerous and many fatal accidents have occurred in the history of their development and operation. Consequently, their design, manufacture, and operation are regulated by engineering authorities backed by legislation. For these reasons, the definition of a pressure vessel varies from country to country, but involves parameters such as maximum safe operating pressure and temperature.
Uses
Pressure vessels are used in a variety of applications in both industry and the private sector. They appear in these sectors as industrial compressed air receivers and domestic hot water storage tanks. Other examples of pressure vessels are diving cylinder, recompression chamber, distillation towers, autoclaves, and many other vessels in mining or oil refineries and petrochemical plants, nuclear reactor vessel, habitat of a space ship, habitat of a submarine, pneumatic reservoir, hydraulic reservoir under pressure, rail vehicle airbrake reservoir, road vehicle airbrake reservoir and storage vessels for liquified gases such as ammonia, chlorine, propane, butane, and LPG.
Pressure vessel features
Shape of a pressure vessel
Pressure vessels may theoretically be almost any shape, but shapes made of sections of spheres, cylinders, and cones are usually employed. A common design is a cylinder with end caps called heads. Head shapes are frequently either hemispherical or dished (torispherical). More complicated shapes have historically been much harder to analyze for safe operation and are usually far more difficult to construct.
Theoretically, a spherical pressure vessel has approximately twice the strength of a cylindrical pressure vessel.[1] However, a spherical shape is tough to manufacture, therefore more expensive, so most pressure vessels are cylindrical with 2:1 semi-elliptical heads or end caps on each end. Smaller pressure vessels are assembled from a pipe and two covers. A disadvantage of these vessels is that greater breadths are more expensive, so that for example the most economic shape of a 1,000 litres (35 cu ft), 250 bars (3,600 psi) pressure vessel might be a breadth of 914.4 millimetres (36 in) and a width of 1,701.8 millimetres (67 in) including the 2:1 semi-elliptical domed end caps.
Construction materials
Theoretically almost any material with good tensile properties that is chemically stable in the chosen application could be employed. However, pressure vessel design codes and application standards (ASME BPVC Section II, EN 13445-2 etc.) contain long lists of approved materials with associated limitations in temperature range.
Many pressure vessels are made of steel. To manufacture a cylindrical or spherical pressure vessel, rolled and possibly forged parts would have to be welded together. Some mechanical properties of steel, achieved by rolling or forging, could be adversely affected by welding, unless special precautions are taken. In addition to adequate mechanical strength, current standards dictate the use of steel with a high impact resistance, especially for vessels used in low temperatures. In applications where carbon steel would suffer corrosion, special corrosion resistant material should also be used.
Some pressure vessels are made of composite materials, such as filament wound composite using carbon fibre held in place with a polymer. Due to the very high tensile strength of carbon fibre these vessels can be very light, but are much more difficult to manufacture. The composite material may be wound around a metal liner, forming a composite overwrapped pressure vessel.
Other very common materials include polymers such as PET in carbonated beverage containers and copper in plumbing.
Pressure vessels may be lined with various metals, ceramics, or polymers to prevent leaking and protect the structure of the vessel from the contained medium. This liner may also carry a significant portion of the pressure load.[2][3]
Scaling
No matter what shape it takes, the minimum mass of a pressure vessel scales with the pressure and volume it contains and is inversely proportional to the strength to weight ratio of the construction material (minimum mass decreases as strength increases[4]).
Scaling of stress in walls of vessel
Pressure vessels are held together against the gas pressure due to tensile forces within the walls of the container. The normal (tensile) stress in the walls of the container is proportional to the pressure and radius of the vessel and inversely proportional to the thickness of the walls.[5] Therefore pressure vessels are designed to have a thickness proportional to the radius of tank and the pressure of the tank and inversely proportional to the maximum allowed normal stress of the particular material used in the walls of the container.
Because (for a given pressure) the thickness of the walls scales with the radius of the tank, the mass of a tank (which scales as the length times radius times thickness of the wall for a cylindrical tank) scales with the volume of the gas held (which scales as length times radius squared). The exact formula varies with the tank shape but depends on the density, ρ, and maximum allowable stress σ of the material in addition to the pressure P and volume V of the vessel. (See below for the exact equations for the stress in the walls.)
Spherical vessel
For a sphere, the mass of a pressure vessel is
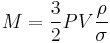 ,
,
where
 is mass,
is mass, is the pressure difference from ambient (the gauge pressure),
is the pressure difference from ambient (the gauge pressure), is volume,
is volume, is the density of the pressure vessel material,
is the density of the pressure vessel material, is the maximum working stress that material can tolerate.[6]
is the maximum working stress that material can tolerate.[6]
Other shapes besides a sphere have constants larger than 3/2 (infinite cylinders take 2), although some tanks, such as non-spherical wound composite tanks can approach this.
Cylindrical vessel with hemispherical ends
This is sometimes called a "bullet" for its shape.
For a cylinder with hemispherical ends,
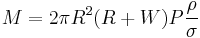 ,
,
where
- R is the radius
- W is the middle cylinder width only, and the overall width is W + 2R
2:1 Cylindrical vessel with semi-elliptical ends
In a vessel with an aspect ratio of middle cylinder width to radius of 2:1,
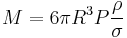 .
.
Gas storage
In looking at the first equation, the factor PV, in SI units, is in units of (pressurization) energy. For a stored gas, PV is proportional to the mass of gas at a given temperature, thus
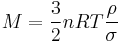 . (see gas law)
. (see gas law)
The other factors are constant for a given vessel shape and material. So we can see that there is no theoretical "efficiency of scale", in terms of the ratio of pressure vessel mass to pressurization energy, or of pressure vessel mass to stored gas mass. For storing gases, "tankage efficiency" is independent of pressure, at least for the same temperature.
So, for example, a typical design for a minimum mass tank to hold helium (as a pressurant gas) on a rocket would use a spherical chamber for a minimum shape constant, carbon fiber for best possible 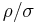 , and very cold helium for best possible
, and very cold helium for best possible 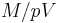 .
.
Stress in thin-walled pressure vessels
Stress in a shallow-walled pressure vessel in the shape of a sphere is
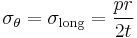 ,
,
where 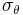 is hoop stress, or stress in the circumferential direction,
is hoop stress, or stress in the circumferential direction, 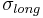 is stress in the longitudinal direction, p is internal gauge pressure, r is the inner radius of the sphere, and t is thickness of the cylinder wall. A vessel can be considered "shallow-walled" if the diameter is at least 10 times (sometimes cited as 20 times) greater than the wall depth.[7]
is stress in the longitudinal direction, p is internal gauge pressure, r is the inner radius of the sphere, and t is thickness of the cylinder wall. A vessel can be considered "shallow-walled" if the diameter is at least 10 times (sometimes cited as 20 times) greater than the wall depth.[7]
Stress in a shallow-walled pressure vessel in the shape of a cylinder is
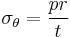 ,
,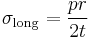 ,
,
where 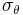 is hoop stress, or stress in the circumferential direction,
is hoop stress, or stress in the circumferential direction, 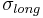 is stress in the longitudinal direction, p is internal gauge pressure, r is the inner radius of the cylinder, and t is thickness of the cylinder wall.
is stress in the longitudinal direction, p is internal gauge pressure, r is the inner radius of the cylinder, and t is thickness of the cylinder wall.
Almost all pressure vessel design standards contain variations of these two formulas with additional empirical terms to account for wall thickness tolerances, quality control of welds and in-service corrosion allowances.
For example, the ASME Boiler and Pressure Vessel Code (BPVC) (UG-27) formulas are:[8]
Spherical shells:
Cylindrical shells:
where E is the joint efficient, and all others variables as stated above.
Winding angle of carbon fibre vessels
Wound infinite cylindrical shapes optimally take a winding angle of 54.7 degrees, as this gives the necessary twice the strength in the circumferential direction to the longitudinal.[9]
Design and operation standards
Pressure vessels are designed to operate safely at a specific pressure and temperature, technically referred to as the "Design Pressure" and "Design Temperature". A vessel that is inadequately designed to handle a high pressure constitutes a very significant safety hazard. Because of that, the design and certification of pressure vessels is governed by design codes such as the ASME Boiler and Pressure Vessel Code in North America, the Pressure Equipment Directive of the EU (PED), Japanese Industrial Standard (JIS), CSA B51 in Canada, Australian Standards in Australia and other international standards like Lloyd's, Germanischer Lloyd, Det Norske Veritas, Société Générale de Surveillance (SGS S.A.), Stoomwezen etc.
Note that where the pressure-volume product is part of a safety standard, any incompressible liquid in the vessel can be excluded as it does not contribute to the potential energy stored in the vessel, so only the volume of the compressible part such as gas is used.
List of standards
- EN 13445: The current European Standard, harmonized with the Pressure Equipment Directive (97/23/EC). Extensively used in Europe.
- ASME Boiler and Pressure Vessel Code Section VIII: Rules for Construction of Pressure Vessels
- BS 5500: Former British Standard, replaced in the UK by BS EN 13445 but retained under the name PD 5500 for the design and construction of export equipment.
- AD Merkblätter: German standard, harmonized with the Pressure Equipment Directive.
- EN 286 (Parts 1 to 4): European standard for simple pressure vessels (air tanks), harmonized with Council Directive 87/404/EEC.
- BS 4994: Specification for design and construction of vessels and tanks in reinforced plastics.
- ASME PVHO: US standard for Pressure Vessels for Human Occupancy
- CODAP: French Code for Construction of Unfired Pressure Vessel
- AS/NZS 1200: Pressure equipment[10]
- API 510[11]
- ISO 11439[12]
- IS 2825-1969 (RE1977)_code_unfired_Pressure_vessels
- FRP tanks and vessels
- AIAA S-080-1998: AIAA Standard for Space Systems - Metallic Pressure Vessels, Pressurized Structures, and Pressure Components
- AIAA S-081A-2006: AIAA Standard for Space Systems - Composite Overwrapped Pressure Vessels (COPVs)
- B51-09 Canadian Boiler, pressure vessel, and pressure piping code
- Stoomwezen: Former pressure vessels code in the Netherlands, also known as RToD: Regels voor Toestellen onder Druk (Dutch Rules for Pressure Vessels)
Leak Before Burst
Leak before burst describes a pressure vessel designed such that a crack in the vessel will grow through the wall, allowing the contained fluid to escape and reducing the pressure, prior to growing so large as to cause fracture at the operating pressure.
Many pressure vessel standards, including the ASME Boiler and Pressure Vessel Code and the AIAA metallic pressure vessel standard, either require pressure vessel designs to be leak before burst, or require pressure vessels to meet more stringent requirements for fatigue and fracture if they are not shown to be leak before burst.[13]
Alternatives to pressure vessels
Depending on the application and local circumstances, alternatives to pressure vessels exist. Examples can be seen in domestic water collection systems, where the following may be used:
- Gravity controlled systems[14] which typically consist of an unpressurized water tank at an elevation higher than the point of use. Pressure at the point of use is the result of the hydrostatic pressure caused by the elevation difference. Gravity systems produce 0.43 pounds per square inch (3.0 kPa) per foot of water head (elevation difference). A municipal water supply or pumped water is typically around 90 pounds per square inch (620 kPa).
- Inline pump controllers or pressure-sensitive pumps.[15]
History of pressure vessels
Large pressure vessels were invented during the industrial revolution, particularly in Great Britain, to be used as boilers for making steam to drive steam engines.
Design and testing standards and a system of certification came about as the result of fatal boiler explosions.
In an early effort to design a tank capable of withstanding pressures up to 10,000 psi (69 MPa), a 6-inch (150 mm) diameter tank was developed in 1919 that was spirally-wound with two layers of high tensile strength steel wire to prevent sidewall rupture, and the end caps longitudinally reinforced with lengthwise high-tensile rods.[16]
See also
- American Society of Mechanical Engineers (ASME)
- Bottled gas
- Composite overwrapped pressure vessel
- Compressed natural gas
- Demister
- Fire-tube boiler
- Gas cylinder
- Gasket
- Head (vessel)
- Minimum Design Metal Temperature (MDMT)
- Pressure bomb - a device for measuring leaf water potentials
- Rainwater harvesting
- Relief valve
- Safety valve
- Shell and tube heat exchanger
- Vapor-Liquid Separator or Knock-Out Drum
- Vortex breaker
- Water well
- Water-tube boiler
Further reading
- Megyesy, Eugene F. (2008, 14th ed.) Pressure Vessel Handbook. PV Publishing, Inc.: Oklahoma City, Oklahoma, USA. www.pressurevesselhandbook.com Design handbook for pressure vessels based on the ASME code.
Notes
- ^ Hearn, E.J. (1997). Mechanics of Materials 1, An Introduction to the Mechanics of Elastic and Plastic Deformation of Solids and Structural Materials - Third Edition. Chapter 9: Butterworth-Heinemann. pp. 199-203. ISBN 0-7506-3265-8.
- ^ NASA Tech Briefs, "Making a Metal-Lined Composite Overwrapped Pressure Vessel", 1 Mar 2005.
- ^ Frietas, O., "Maintenance and Repair of Glass-Lined Equipment", Chemical Engineering, 1 Jul 2007.
- ^ Puskarich, Paul (2009-05-01) (PDF). Strengthened Glass for Pipleine Systems. MIT. http://www.gmic.org/Student%20Contest%20Entries/2007%20Contest%20Entries/26-Paul%20Puskarich%20-%20Glass%20for%20Pipeline%20Systems.pdf. Retrieved 2009-04-17.
- ^ Ferdinand P. Beer, E. Russel Johnston, Jr., and John T. DeWolf. "7.9". Mechanics of Materials (fourth ed.). McGraw-Hill. p. 463. ISBN 780073659350.
- ^ For a sphere the thickness d = rP/2σ, where r is the radius of the tank. The volume of the spherical surface then is 4πr2d = 4πr3P/2σ. The mass is determined by multiplying by the density of the material that makes up the walls of the spherical vessel. Further the volume of the gas is (4πr3)/3. Combining these equations give the above results. The equations for the other geometries are derived in a similar manner
- ^ Richard Budynas, J. Nisbett, Shigley's Mechanical Engineering Design, 8th ed., New York:McGraw-Hill, ISBN 978-0-07-312193-2, pg 108
- ^ An International Code 2007 ASME Boiler & Pressure Vessel Code. The Americal Society of Mechanical Engineers. 2007. http://www.asme.org/kb/standards/bpvc-resources.
- ^ MIT pressure vessel lecture
- ^ "AS 1200 Pressure Vessels". SAI Global. http://infostore.saiglobal.com/store2/Details.aspx?ProductID=356464. Retrieved 14 November 2011.
- ^ "Pressure Vessel Inspection Code: In-Service Inspection, Rating, Repair, and Alteration". API. 2006-06. http://global.ihs.com/doc_detail.cfm?currency_code=USD&customer_id=2125482C4B0A&shopping_cart_id=282428272F4B30344A5A2D58280A&rid=API1&input_doc_number=510&mid=Q023&input_doc_number=510&country_code=US&lang_code=ENGL&item_s_key=00010564&item_key_date=930631&input_doc_number=510&input_doc_title=.
- ^ "Gas cylinders - High pressure cylinders for the on-board storage of natural gas as a fuel for automotive vehicles". ISO. 2006-07-18. http://www.iso.org/iso/catalogue_detail?csnumber=33298. Retrieved 2009-04-17.
- ^ ANSI/AIAA S-080-1998, Space Systems - Metallic Pressure Vessels, Pressurized Structures, and Pressure Components, §5.1
- ^ Pushard, Doug (2005). "Domestic water collection systems also sometimes able to function on gravity". Harvesth2o.com. http://www.harvesth2o.com/faq.shtml. Retrieved 2009-04-17.
- ^ Pushard, Doug. "Alternatives to pressure vessels in domestic water systems". Harvesth2o.com. http://www.harvesth2o.com/pumps_or_tanks.shtml. Retrieved 2009-04-17.
- ^ Ingenious Coal-Gas Motor Tank, Popular Science monthly, January 1919, page 27, Scanned by Google Books: http://books.google.com/books?id=HykDAAAAMBAJ&pg=PA13
References
- A.C. Ugural, S.K. Fenster, Advanced Strength and Applied Elasticity, 4th ed.
- E.P. Popov, Engineering Mechanics of Solids, 1st ed.
- Megyesy, Eugene F. "Pressure Vessel Handbook, 14th Edition." PV Publishing, Inc. Oklahoma City, OK
External links
- Use of pressure vessels in oil and gas industry
- Basic formulas for thin walled pressure vessels; with examples
- ASME Boiler and Pressure Vessel website
- Journal of Pressure Vessel Technology
- EU Pressure Equipment Directive website
- EU Pressure Equipment Directive 97/23/EC categorization software
- EU Simple Pressure Vessel Directive
- EU Classification